标题：基于快速搜索密度峰值的聚类方法
时间：2014/06/27
期刊：SCI
摘要
聚类分析的目的是根据元素的相似性将其分类。它的应用范围从天文学到生物信息学、文献计量学和模式识别。我们提出了一种基于这样一种思想的方法，即簇中心的密度比它们的邻居高，并且与高密度点的距离相对较大。这一思想构成了聚类过程的基础，在这个过程中，聚类的数量会直观地产生，离群值会自动被发现并排除在分析之外，而不管聚类的形状和嵌入的空间的维数如何，聚类都会被识别出来。我们在几个测试用例上展示了该算法的强大功能。
分析1
分析2
第一步：（生成距离矩阵） 计算一个样本点与其他m-1个样本点的距离，产生了一个mxm大小的矩阵。该矩阵有两个特点：一、主对角线上的元素为0，因为自身到自身的距离是0。二、是对称矩阵，因为a点到b点的距离等于b点到a点的距离。
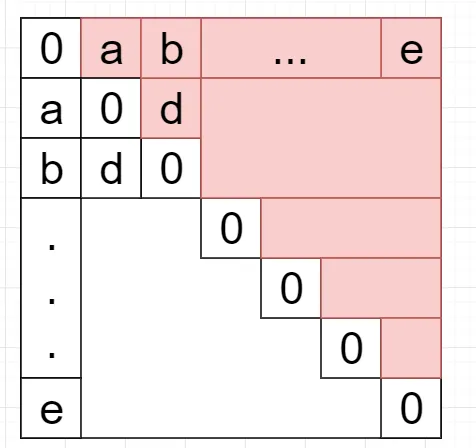
**第二步：（获取截断距离dc） ** 将上图中红色部分的元素取出，放入列表。一共有m(m-1)/2个元素。对列表进行升序排序，取前t%的距离值。例如:对于列表[1,2,3…,99,100]，取2%的距离值，那么dc就为2。所以dc是一个标量。
第三步：（求每个样本点的密度值） 在参考文章中，有两种计算密度的方法，文章中采用的第一种 Cut-off kernel 方法
求解局部密度的两种方法
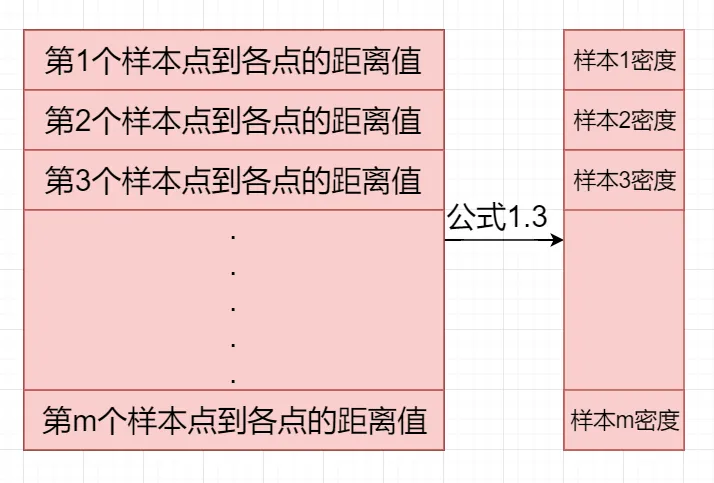
由于我们之前求得了mxm的距离矩阵，那么矩阵的每一行就代表样本点到各个点的距离。例如，求第i行的样本点的密度值，可以将第i行的数据套用1.3的公式，就会得到一个标量，那么该标量就是该样本的密度值，所以若对所有点求它们的密度值，可以得到一个mx1的向量density。
第四步：（求每个样本点的“上级”） ** 每个样本点“上级”的定义为：比当前样本点的密度要大，在密度大的样本点中选择离自己最近的那个点作为自己的上级。**例如样本点[1,2,3,4]，比1密度大的点有3,4。而在距离信息中，4比3更靠近1，那么4就是1的”上级”。若是密度最大那个点，则上级是其自身。在该步骤中，要记录2个大小为mx1的向量信息。一个向量cloest_leader存储当前样本的“上级”，另一个向量delta_ls存储“上级”距离自身的距离，那么密度最大点的距离值记为距离矩阵中最大的那个值。
第五步：（根据r值人工设置分类的簇数） 根据上述步骤，我们已经求得了样本点距离向量detal_ls和密度向量density。根据公式
将点乘得到大小为mx1的向量记为score。我们希望r值越大越好，决定最终簇的分类数量。还是要人工选择，这也是这个算法automatically被喷的比较厉害的地方。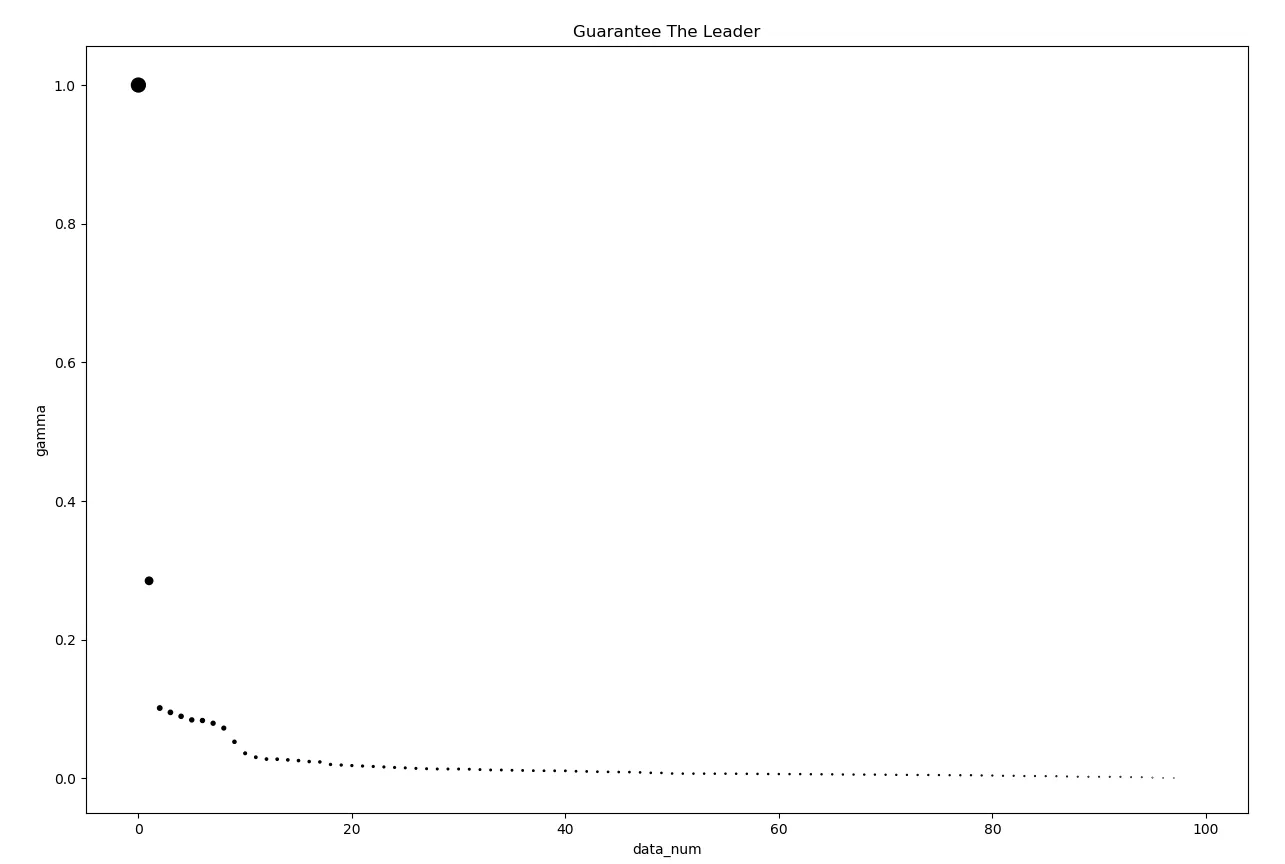
第六步：（选择k个类别） 由于上个步骤，我们人工设置了簇的类别数为2，那么应该选取2个最终类别。首先对score向量进行升序排序，选取最大值的下标作为最终类别。假设得到的最终类别为[5,11]。
第七步：（为每个样本点分配类别） 最后我们要为m个样本点分配它们所属的类别了，记得之前步骤得到的记录每个样本点“上级”的cloest_leader向量嘛。例如1样本点的上级可能是3，那么我们还是要去3的上级是谁，可能3的上级是11。那么就停止寻找，此时1的类别就是11了。有点像给一个小兵分类，先问他的排长是谁，再问他的团长是谁，直到找到他所属的司令，才停止寻找，给小兵打上司令的标签。所以最终得到类别所属向量里面的元素只有5和11。例如[5,5,11,11,5,11,…,11,5]。这样我们就将所有的样本点都进行了分类，而且得到了两个簇。
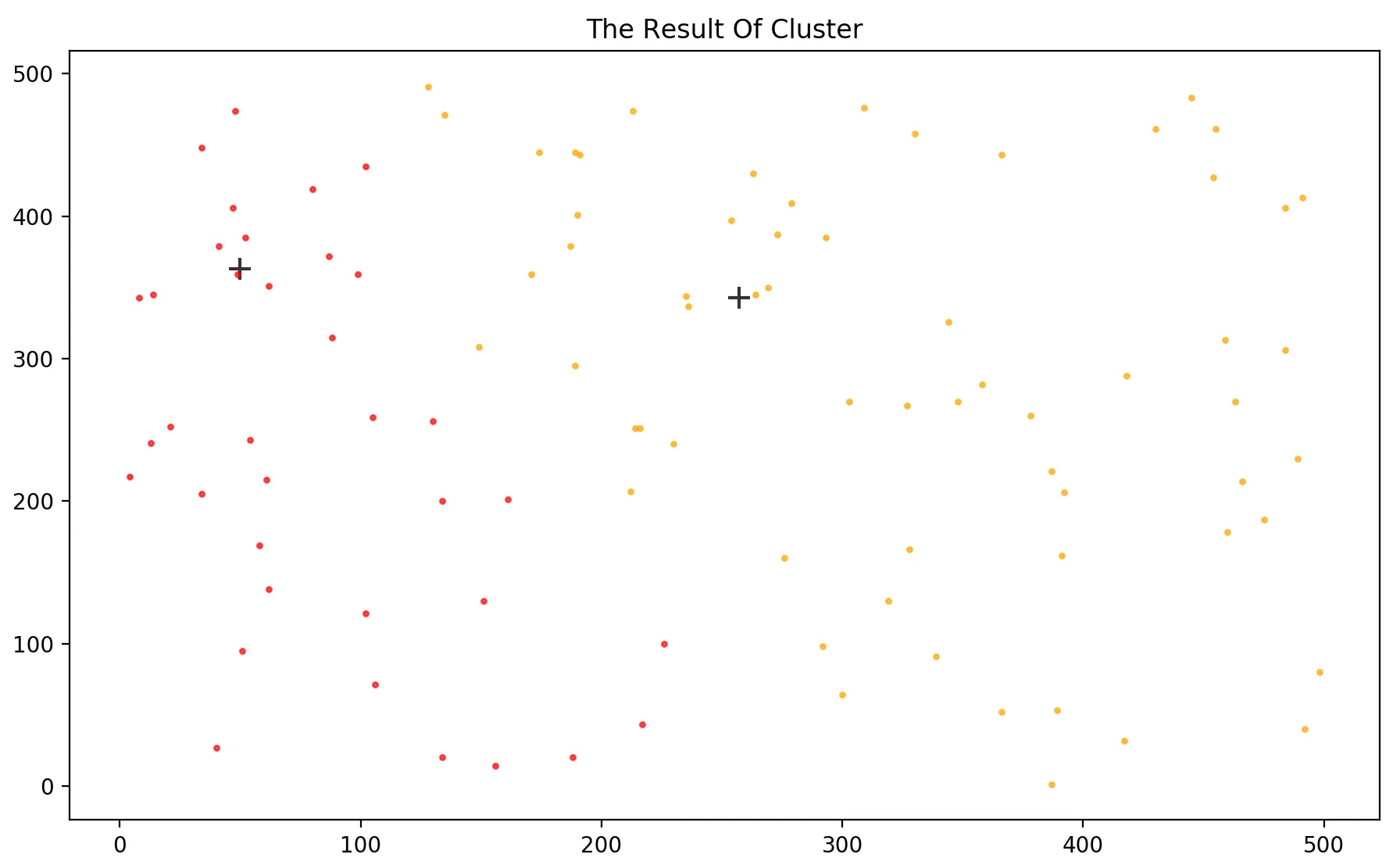
分析3
由Alex Rodriguez和Alessandro Laio发表的《Clustering by fast search and find of density peaks》的主要思想是寻找被低密度区域分离的高密度区域。
基于这样的一种假设：对于一个数据集，聚类中心被一些低局部密度的数据点包围，而且这些低局部密度的点距离其他有高局部密度的点的距离都比较大。
分析4
优点：
- 快速高效
缺点：
- dc 的值需要手动仔细确定
汇报稿子：
