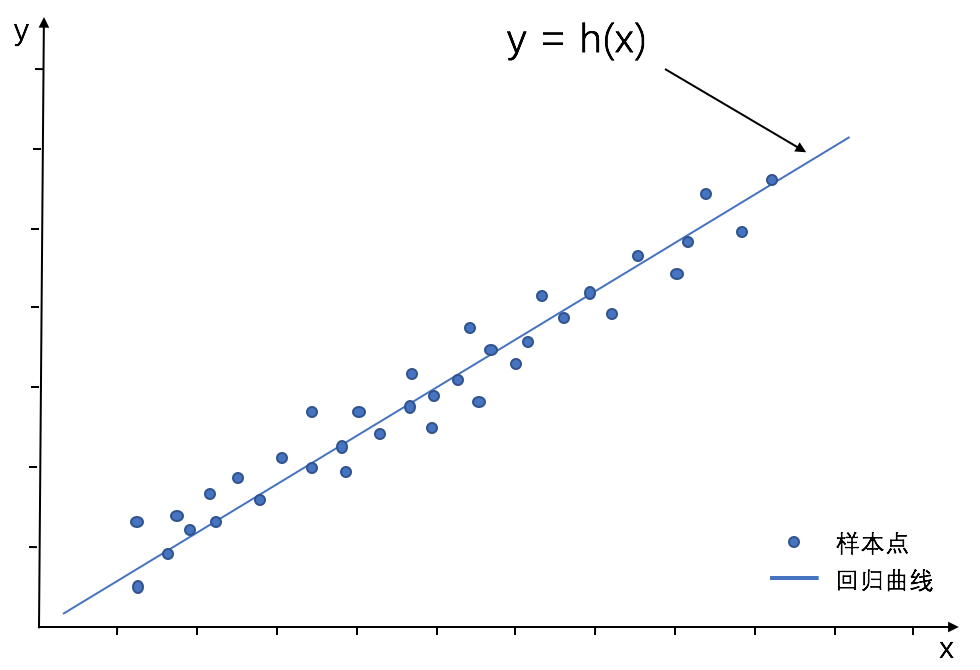
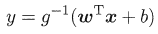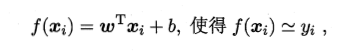第3章 线性模型
3.1 基本形式
什么是线性模型?他能做什么?它的优点?
- 定义:

- 优点:
- 形式简单、易于建模,但却蕴含着机器学习中一些重要的基本思想,许多功能更为强大的非线性模型可以在线性模型的基础上通过引入层级结构或高维映射而得。
- ω 直观的表达了各属性在预测中的重要性,因此线性模型有更好的解释性。
- 例:
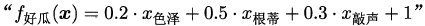
- 例:
- 常见的分类:
- 回归任务
- 线性回归(3.2)
- 分类任务
- 对数几率回归(3.3)
- 线性判别分析(3.4)
- 多分类任务
- 多分类学习(3.5)
- 回归任务
3.2 线性回归
问题转化:
预测数据 —-> 求线性函数 —-> 求 ω 和 b —-> 让均方误差最小
3.2.1 一元线性回归
定义 / 特点:
- 只有一个属性,即 d = 1
- ω 和 b 是一个数
ω 和 b 求解过程:
- 1、

- 2、核心:确定 ω 和 b 的关键在于 f(x) 与 y 之间差别
- 3、

- 4、求导:
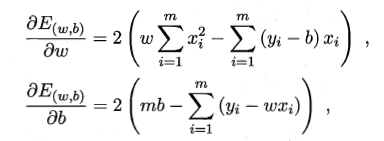
- 5、得到最优解的闭式:
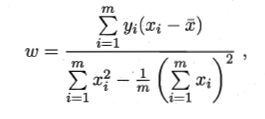
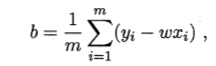
- 1、
补充:
- 均方误差:(实际值 - 预测值)的平均值
- 均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称“欧氏距离”。
- 最小二乘法:基于均方误差最小化来进行的模型求解的方法称为”最小二乘法“,在线性回归中,最小二乘法就是试图找到一条直线,使所有样本到直线的欧氏距离之和最小。
3.2.2 多元线性回归
定义 / 特点:
- 不止一个属性,即 d > 1
- ω 和 b 是矩阵(一组数)
求解过程:

最终学得多元线性回归模型为
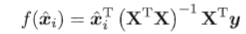

3.2.3 对数线性回归
- 原型:
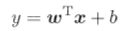
- 对数:
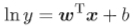
- 意义:它实际是上是在试图让
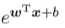 逼近 y. 虽然在函数式形式上是线性回归,但实质上已经是在求取输入空间到输出空间的非线性函数映射。
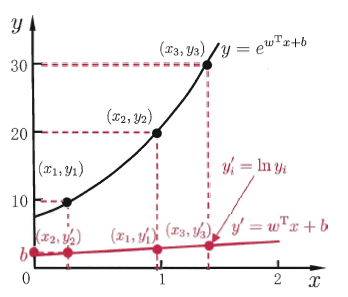
逼近 y. 虽然在函数式形式上是线性回归,但实质上已经是在求取输入空间到输出空间的非线性函数映射。 - 示意图:这里的对数函数起到了将线性回归模型的预测值与实际标记联系起来的作用。
3.2.4 广义线性回归
意义:更广义的的线性模型,对数线性模型是 g( · ) = ln( · ) 时的特例。
形式: