第5章 神经网络
5.4 全局最小与局部极小
误差 E 也可以看作关于连接权 ω 和阈值 θ 的函数,此时神经网络的训练过程可以看作一个寻优过程,即在参数中间,寻找参数使得 E 最小。
局部极小:局部极小解是参数空间中的某个点,其邻域点的误差函数值均不小于该点的函数值。
全局最小:全局最小解则是指参数空间中所有的点的误差函数值均不小于该点的误差函数值。
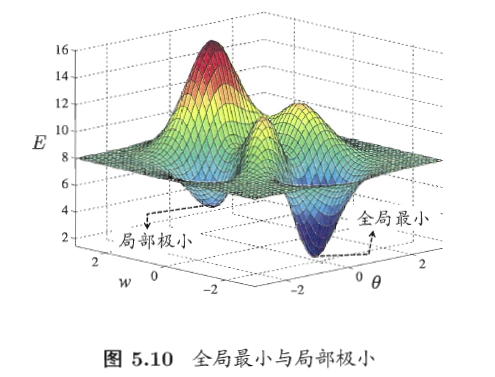
可能存在多个局部极小值,但却只会有一个全局最小值。
“ 全局最小 ” 一定是 “ 局部极小 ”;但“局部极小 ” 不一定是“全局最小 ”。
因此我们的目标是找到 “ 全局最小 ”。
- 如何找到全局最小?——基于梯度的搜索
- 沿着梯度下降方向搜索最优解,若当前点的梯度为零,则已达到局部极小,更新量为零,这意味着参数的迭代更新在此停止。
- 显然,如果误差函数仅有一个局部极小,那么此时找到的局部极小就是全局最小;
- 然而,如果误差函数具有多个局部极小,该怎么办?
- 以多组不同初始值参数初始化多个神经网络 / 使用随机梯度下降


- 上述跳出局部极小的技术大多是启发式,理论上尚缺乏保障。
- 沿着梯度下降方向搜索最优解,若当前点的梯度为零,则已达到局部极小,更新量为零,这意味着参数的迭代更新在此停止。
5.5 其他常见神经网络
5.5.1 RBF( 径向基函数 )网络
- BP 网络
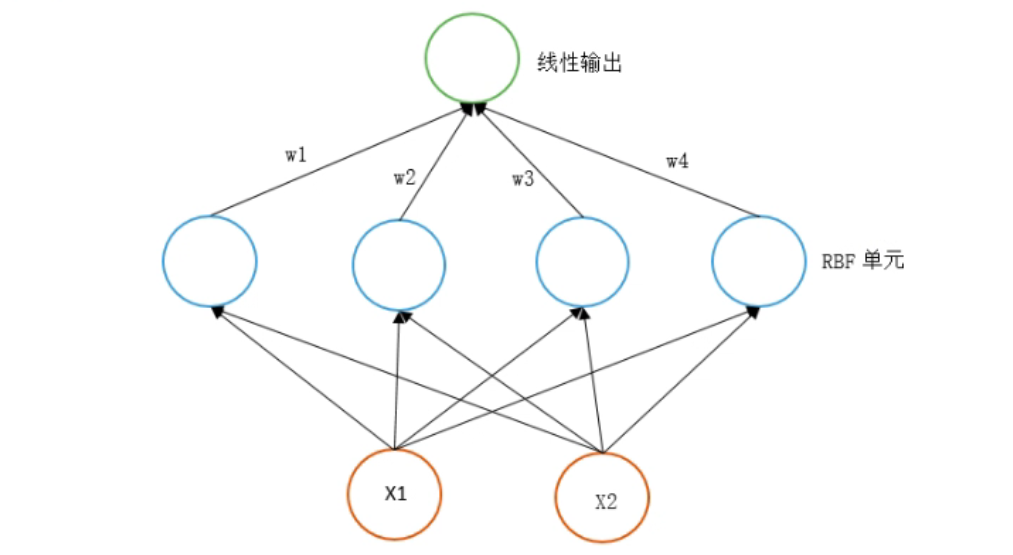
- RBF 网络:
径向基函数:是一个取值仅依赖于到原点距离的实值函数。此外,也可以按到某一中心点c的距离来定义。
RBF 网络结构:RBF Network 通常只有三层。输入层、中间层计算输入 x 矢量与样本矢量 c 欧式距离的值,输出层算它们的线性组合。
训练 RBF 网络步骤:
- 第一步,确定神经元中心,常用的方法包括随机采样、聚类。
- 第二步,利用 BP 算法来确定参数。

RBF 与 BP 最重要的区别:
1 中间层神经元的区别。
- RBF: 神经元是一个以gaussian函数为核函数的神经元。
2 中间层数的区别。
- 中间层只有一层。经过训练后每一个神经元得以确定输入权重:即每一个神经元知道要在什么样的输入值下引起最大的响应。
3 运行速度的区别。
- 原因是因为层数,层数越少,需要确定的权重(weight)越少,越快。
- 为什么三层可以做这么多层的事儿?原因是核函数的输出: 是一个局部的激活函数。在中心点那一点有最大的反应;越接近中心点则反应最大,远离反应成指数递减。
5.5.2 ART(自适应谐振理论)网络
- 竞争型学习:是神经网络中一种常用的无监督学习策略,在使用该策略时,网络的输出神经元相互竞争,每一时刻仅有一个竞争获胜的神经元被激活,其他神经元的状态被抑制,这种机制也称 “胜者通吃” 原则。ART 就是竞争型学习的重要代表。
- ART 网络:该网络由比较层、识别层、识别阈值和重置模块构成。
- 比较层:负责接收输入样本,并将其传递给识别层神经元。
- 识别层:识别层每个神经元对应一个模式类,神经元数目可在训练过程中动态增长以增加新的模式类。

.jpg)
- 阈值:显然,识别阈值对 ART 网络的性能有重要影响,当识别阈值较高时,输入样本会被分成较多、较精细的模式类,而如果识别阈值较低,则会产生比较少、比较粗略的模式类。
- ART 优点:可进行增量学习或在线学习。
神经元之间的距离?

