- 梯度下降基本流程:① 在目标函数(损失函数)上随机选择一个初始点。② 通过迭代运算,一步步逼近(损失)函数最小值点。怎么找到最小值的:找到梯度和步长,一步步迭代;像盲人下山一样,用拐棍试探着下。
- w(t+1) = w(t) - η( ∂(l) / ∂(w) )
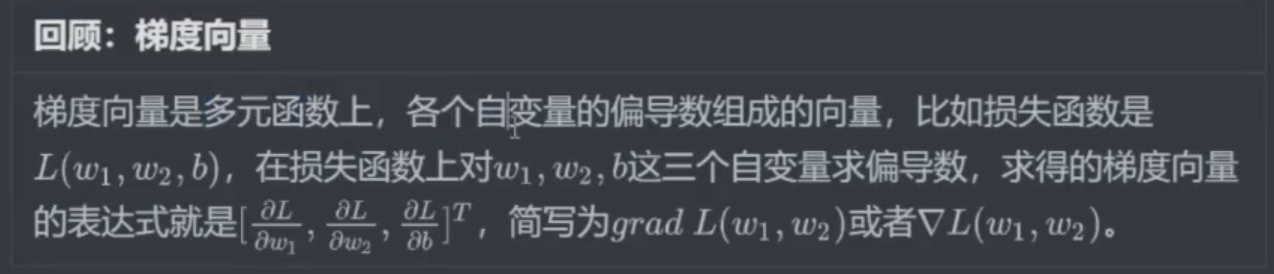
- 梯度:目标函数对所有偏导数的向量;步长:学习率 * 梯度
一、梯度下降中的两个关键问题
梯度下降目的:
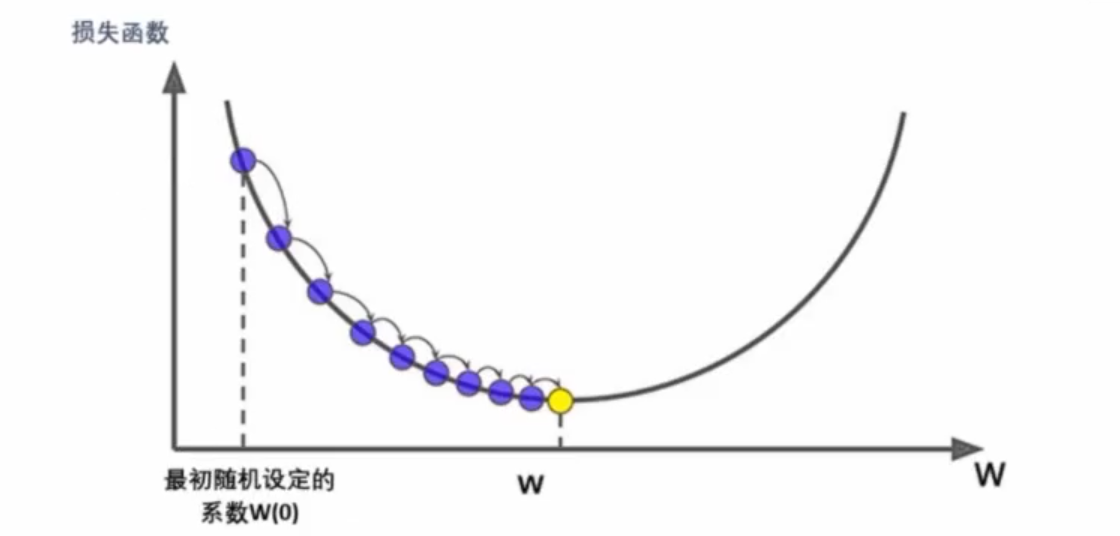
流程:
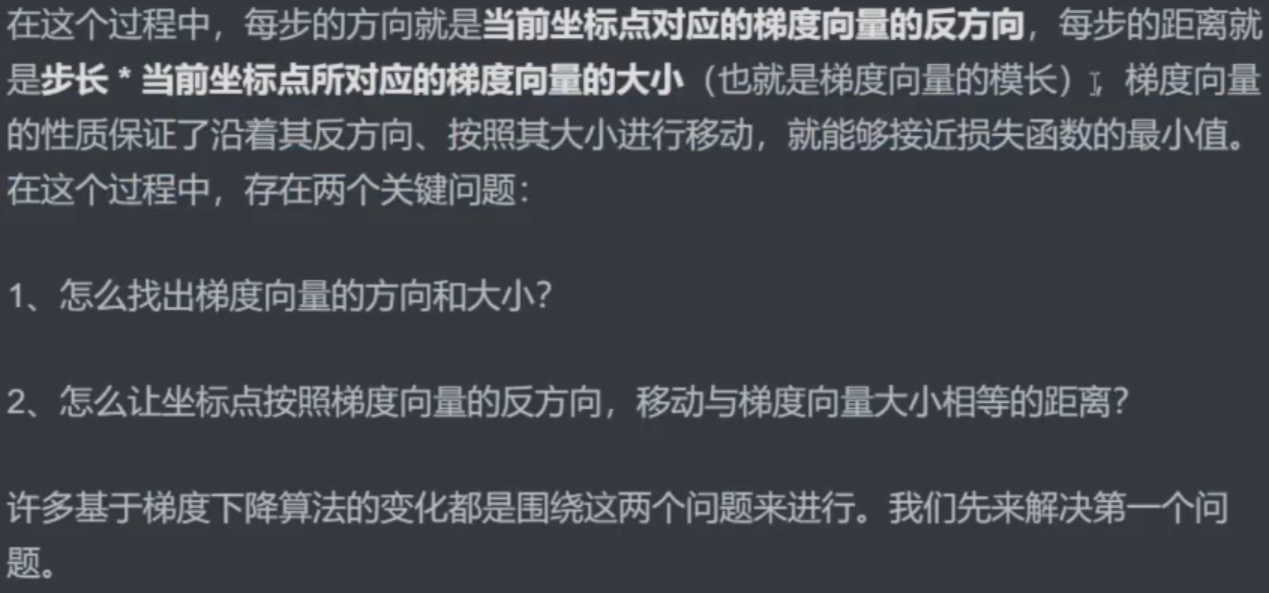
1.1 怎么找出梯度向量的方向和大小


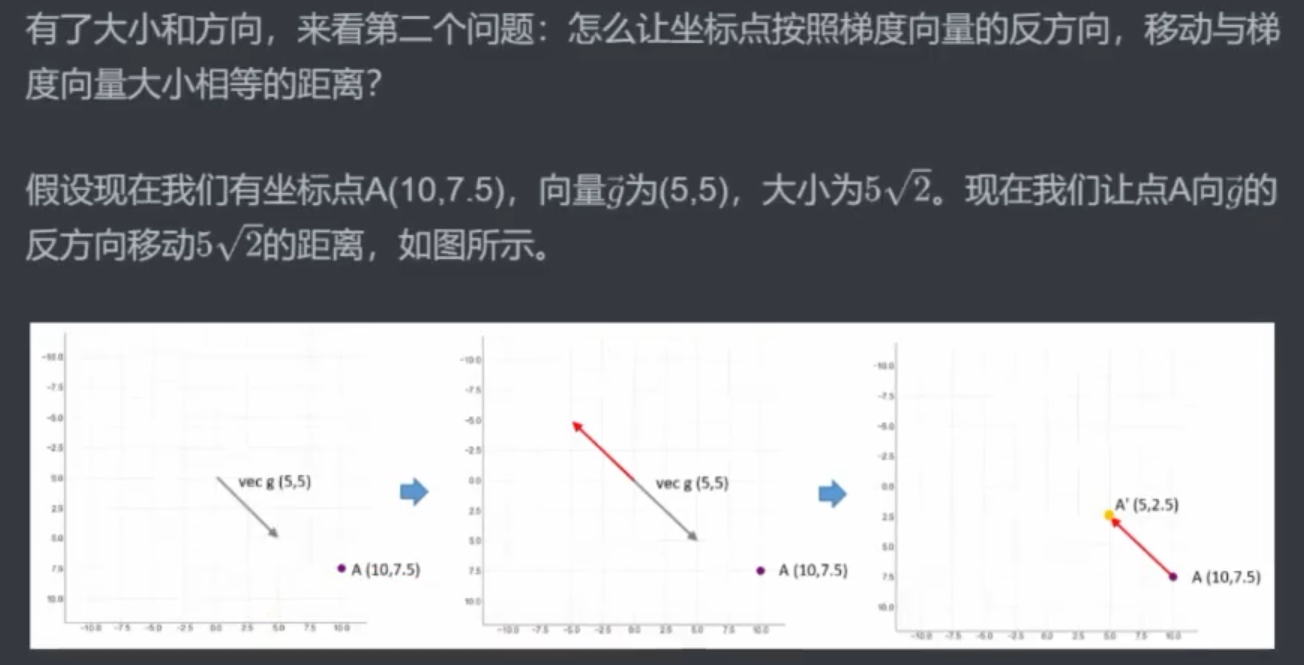
1.2 让坐标点动起来




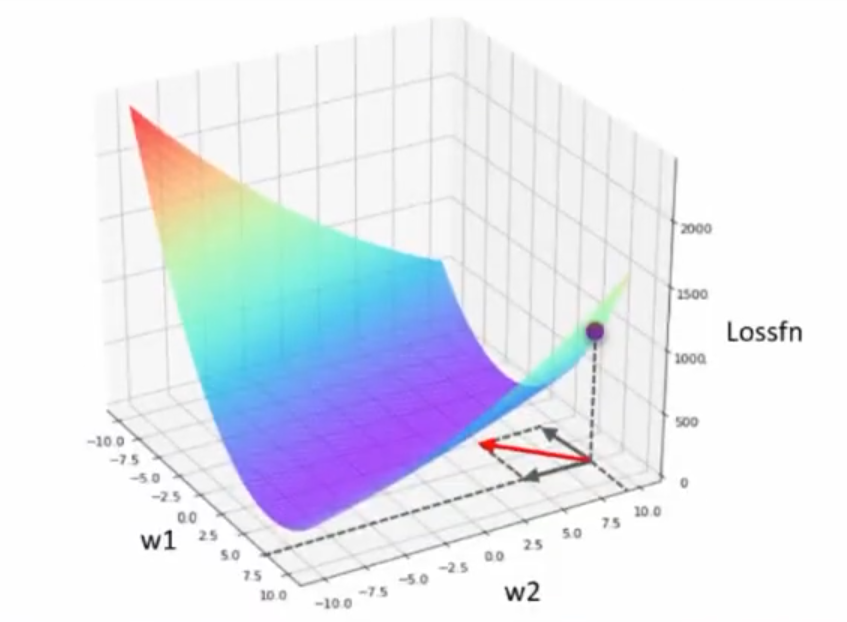
注意:
梯度的方向总是比整体函数少一个维度!
二、找出距离和方向:反向传播
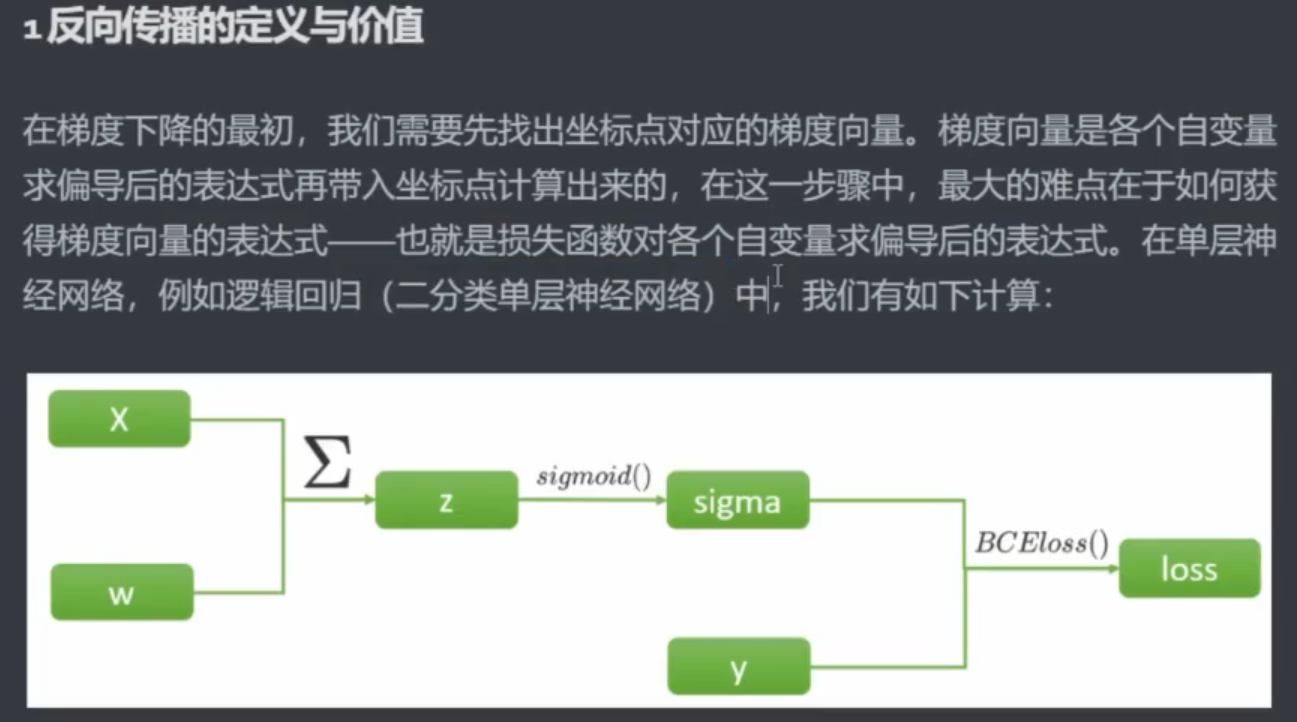
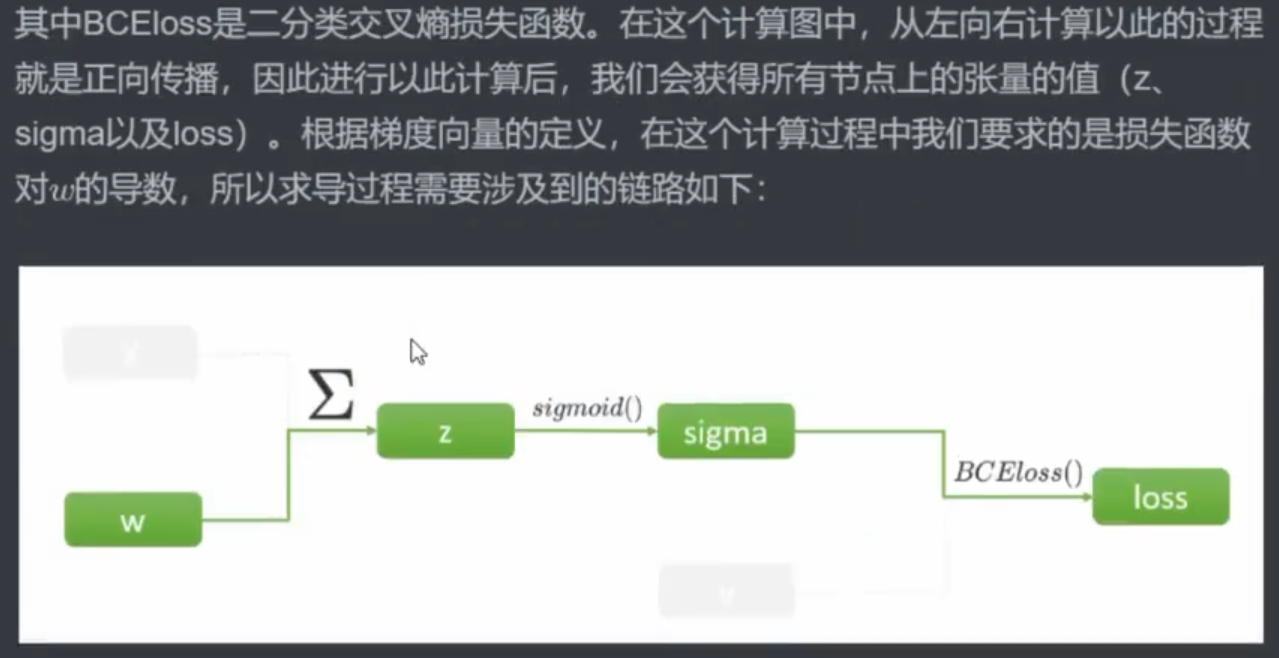

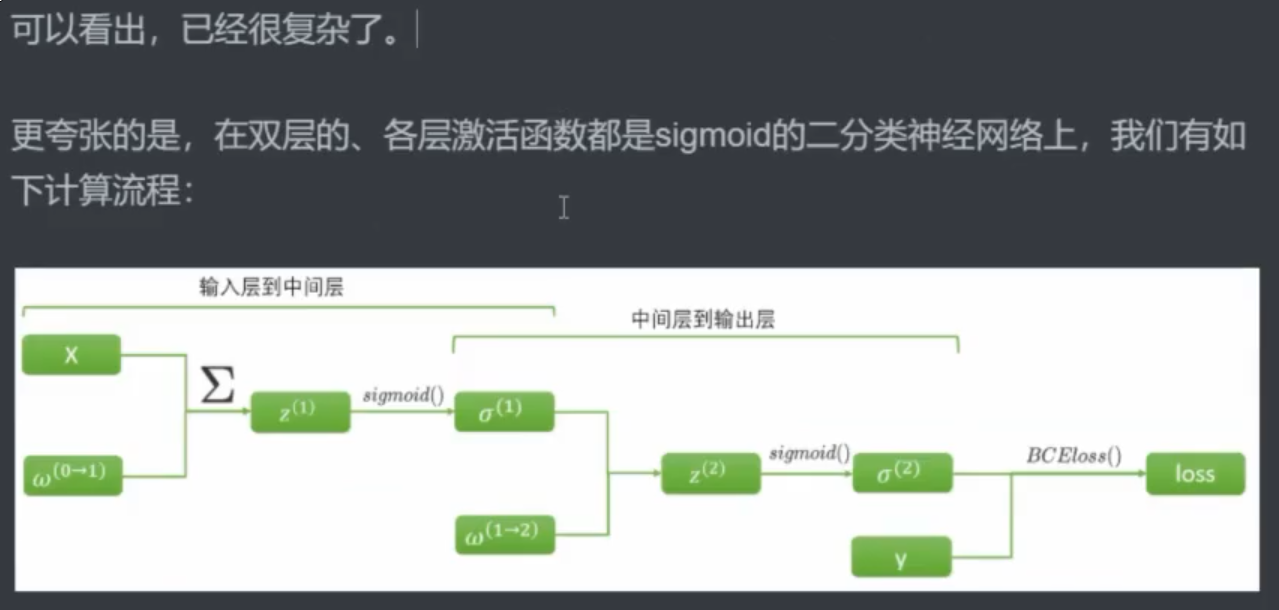
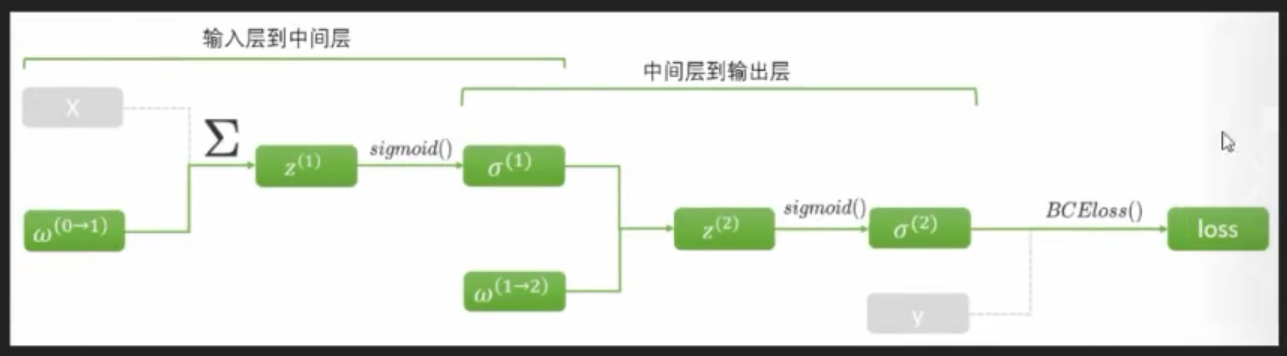

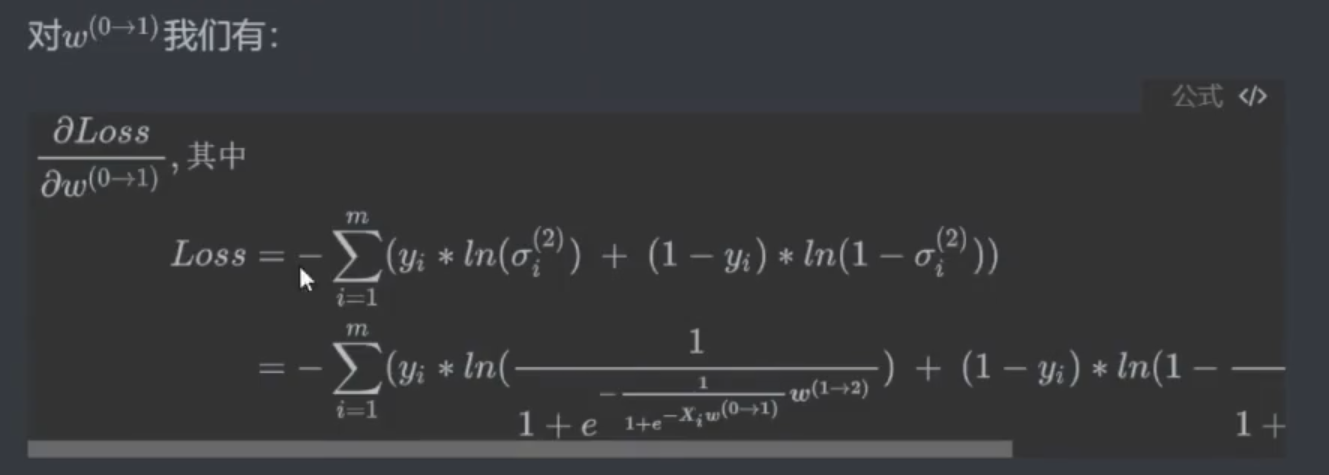

2.1 反向传播理论

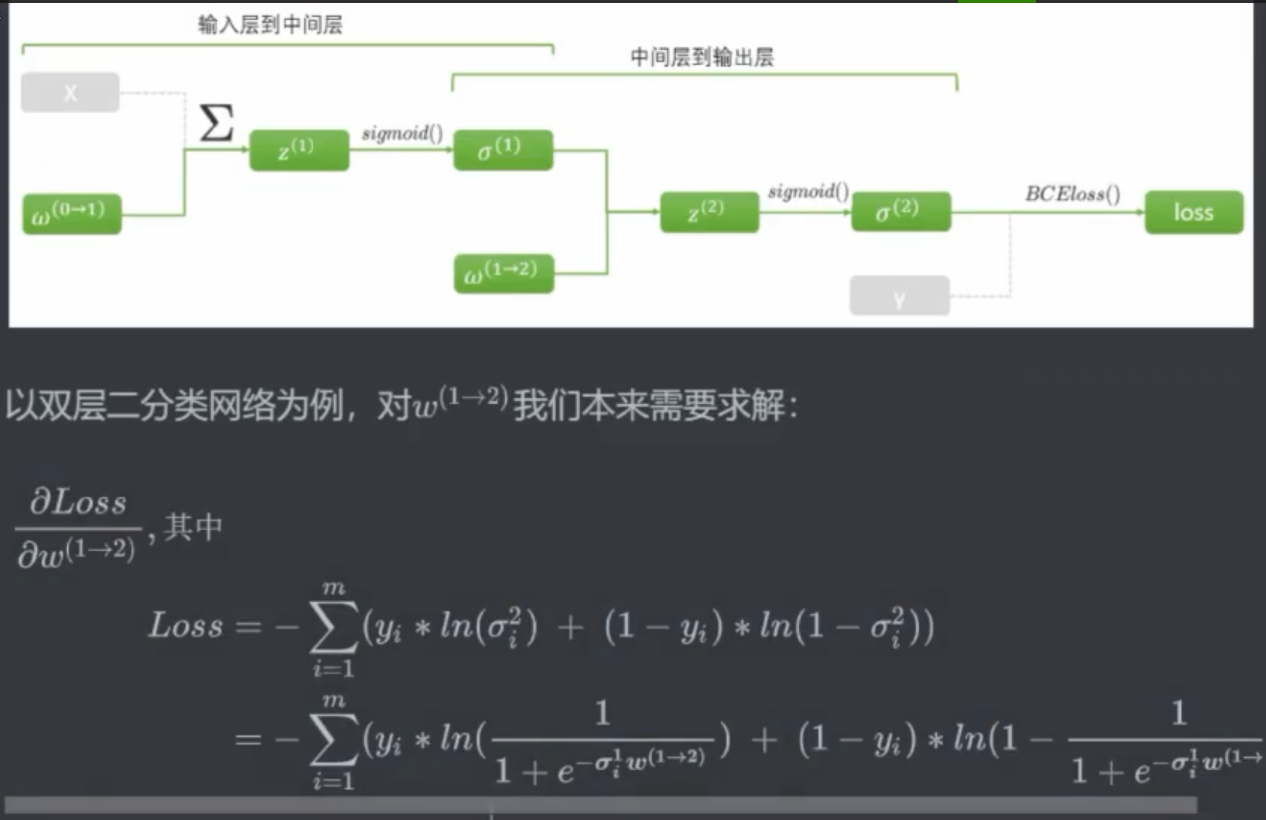

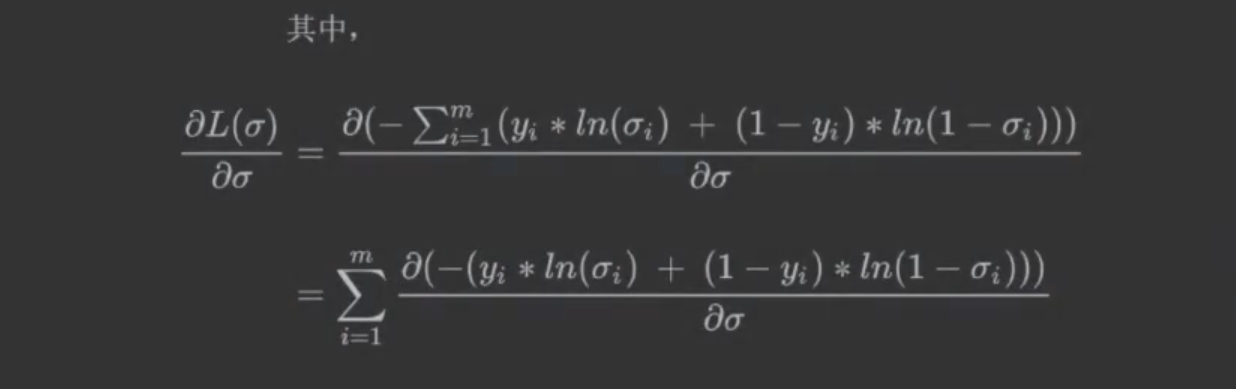
求导不影响加和,可以先加和再求导,也可以先求导再加和,所以可以先将Σ拿出来。


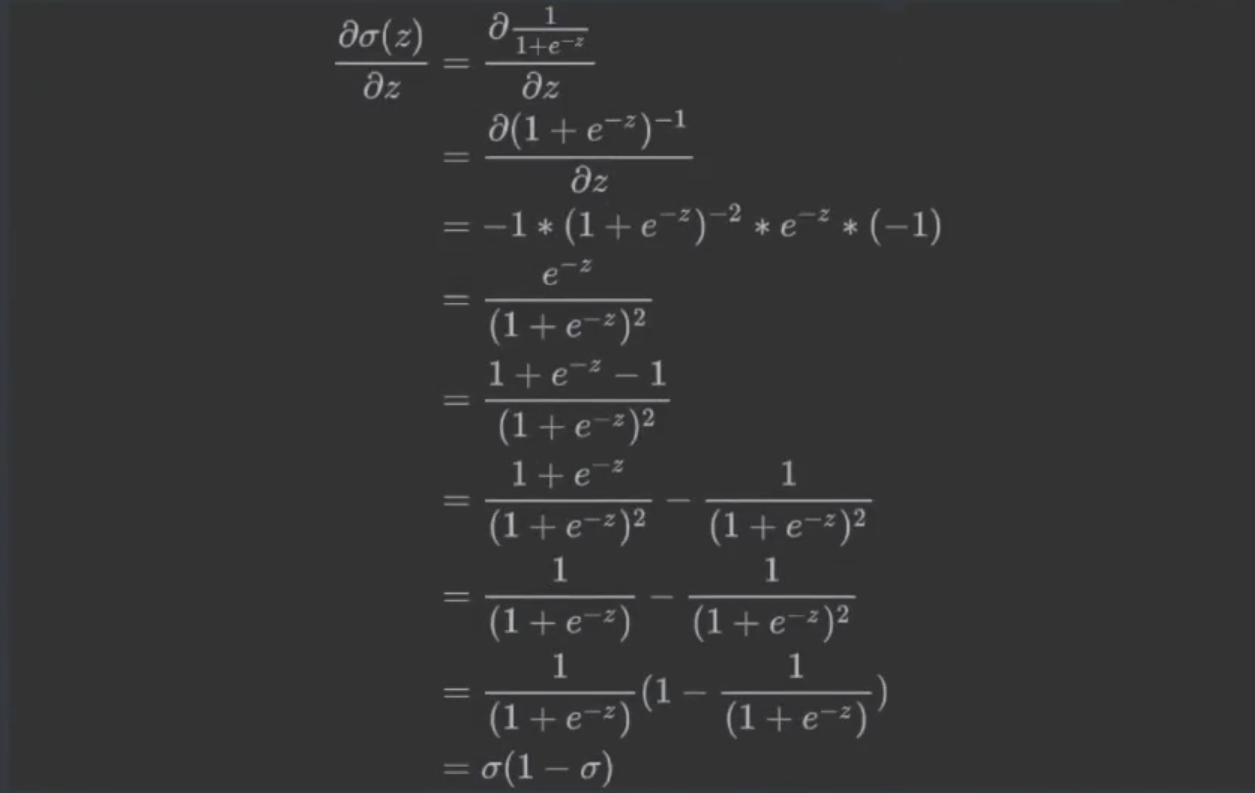
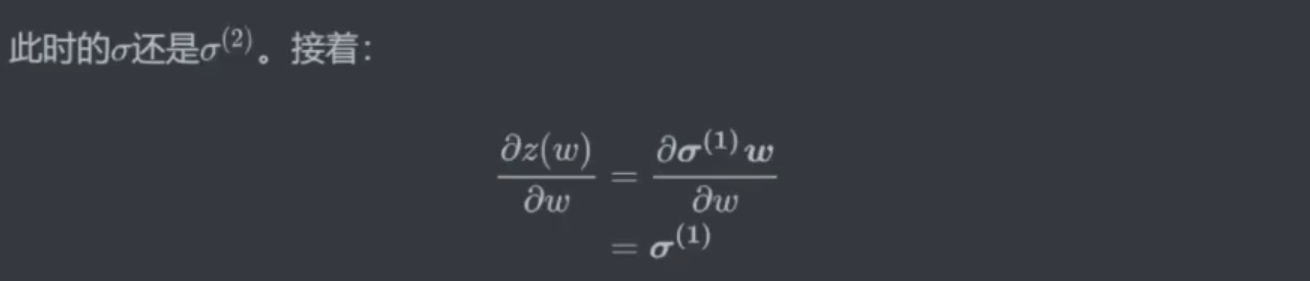

正向传播:计算损失函数(SSE 或其他)(计算过程中算出
zσw)反向传播:算梯度值——偏导数(链式法则需要正向传播时计算出的
zσw)

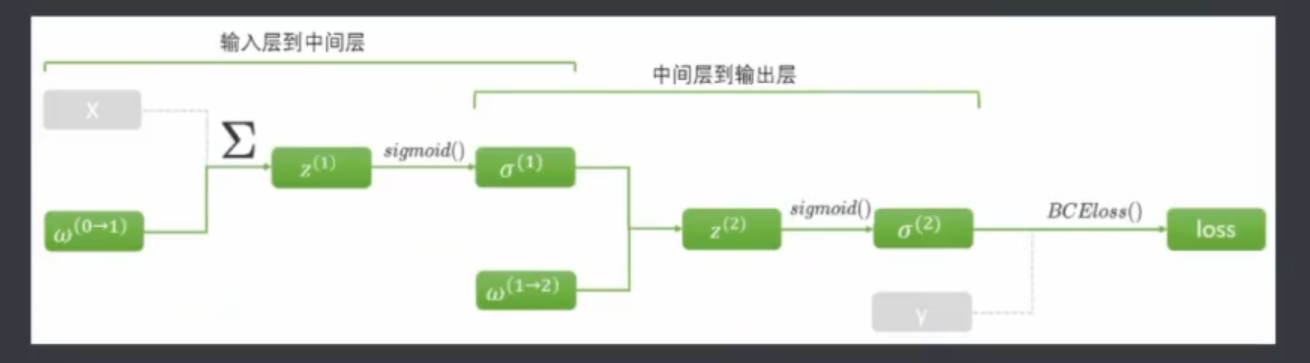


2.2 Pytorch实现反向传播
2.2.1 正向传播
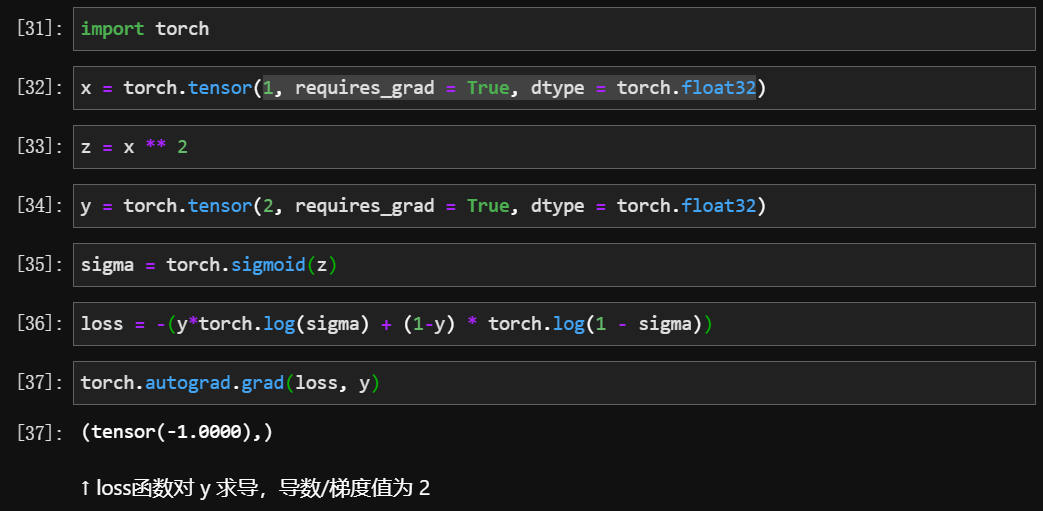
结合以前正向传播的内容,实现反向传播的例子
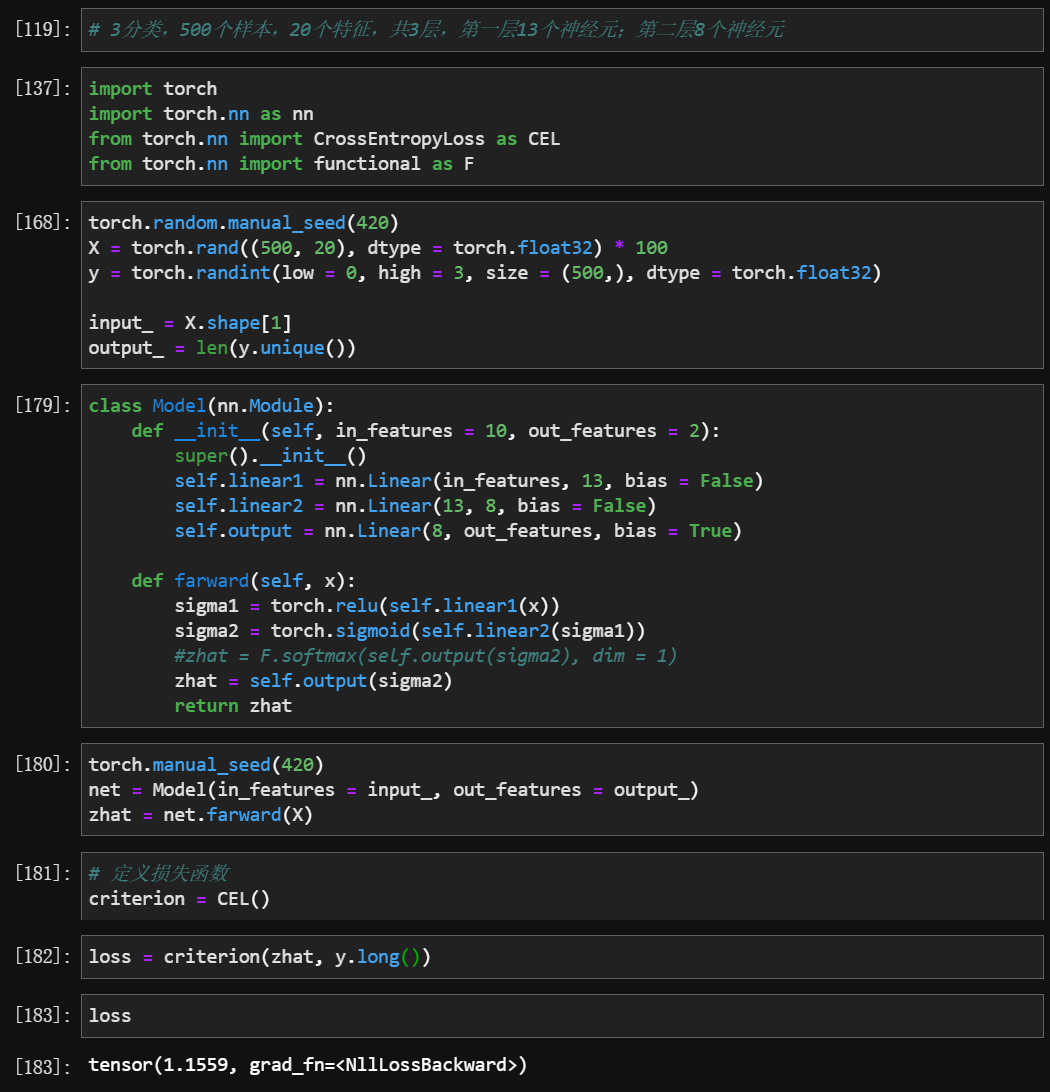
上面这一段是以前正向传播的全部内容
2.2.2 反向传播

loss.backward(retain_graph = True)参数表示:默认
False,True表示运行反向传播后不销毁计算图,即可以重复运行反向传播



2.2.3 迭代w
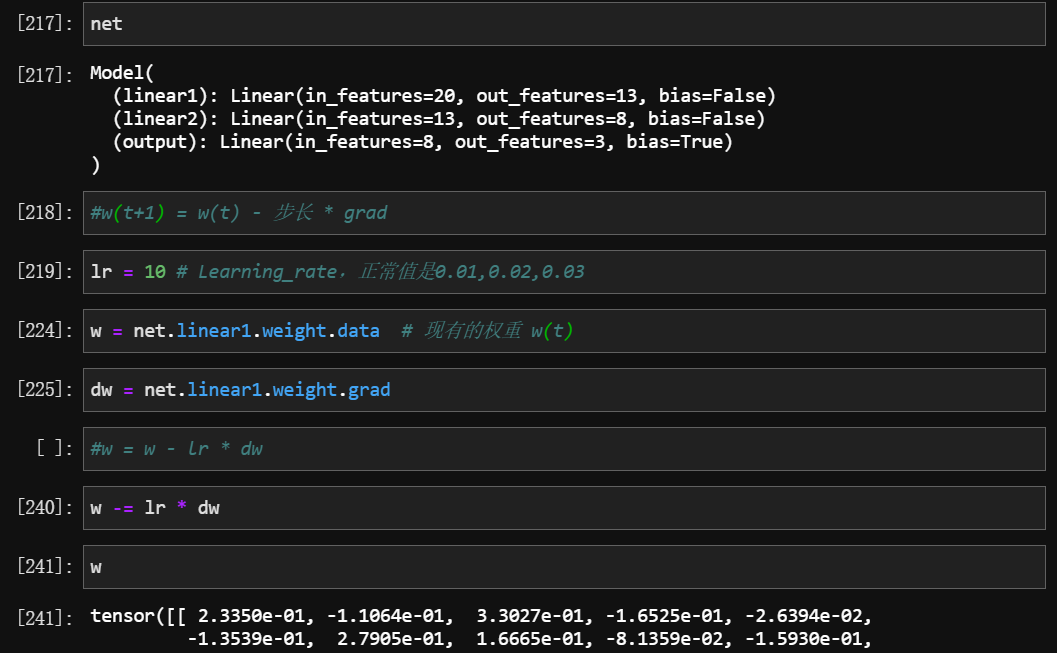
为什么是
net.linear1.weight.data而不是net.linear1.weight因为后者有一些附加信息,前者才是纯数据。
2.2.4 加速迭代 动量法Momentum
学习率低的时候,迭代速度非常慢,有什么好的办法加速迭代吗?


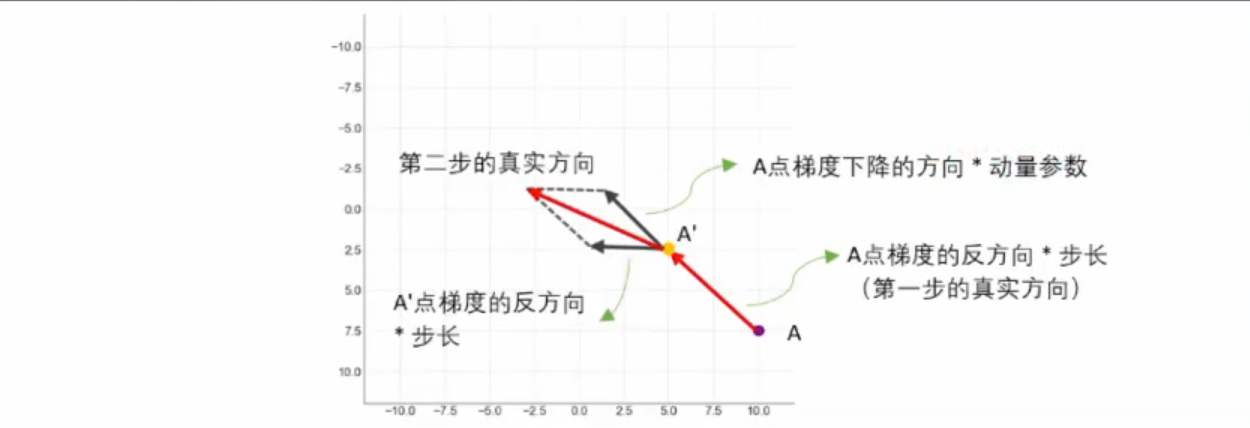


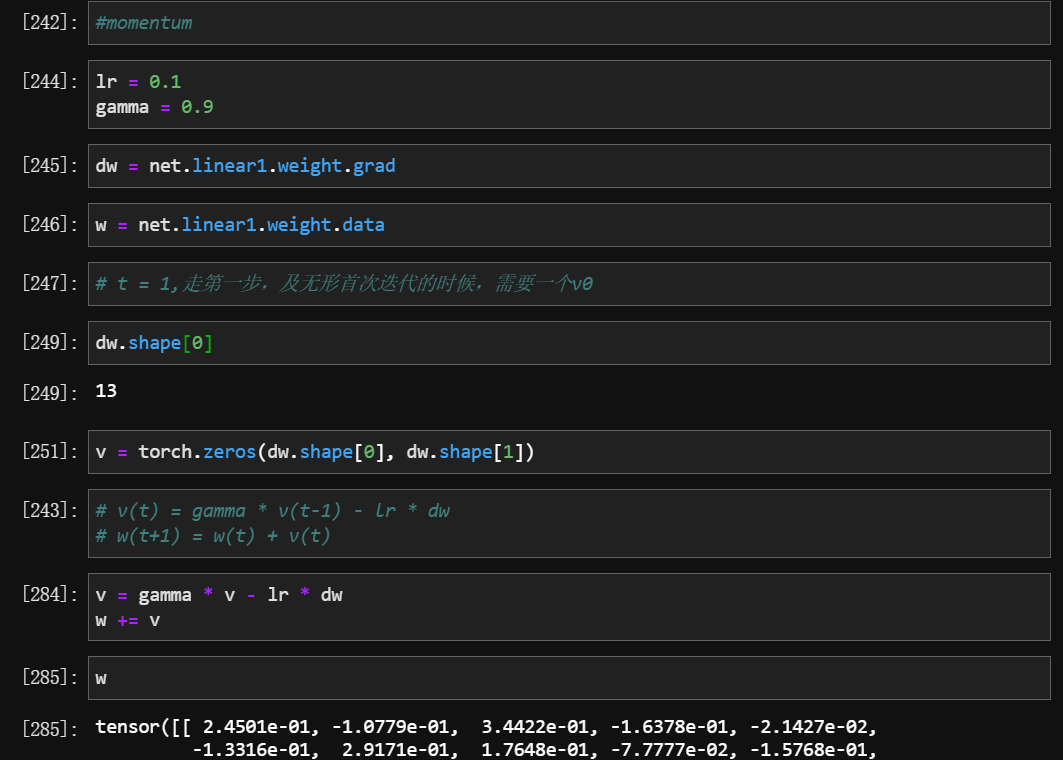
- 自己实现
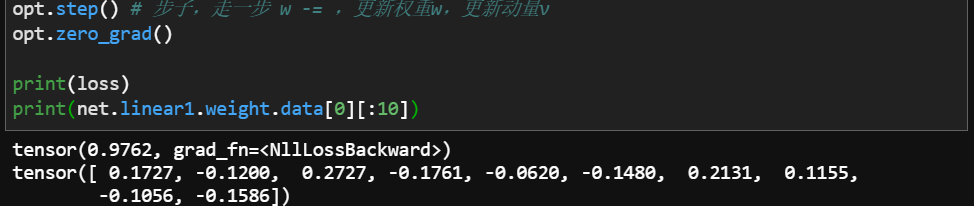
- Pytorch 自带模块实现


2.3 总结:实现一轮梯度下降的全流程
1 | # 1.导入库 |

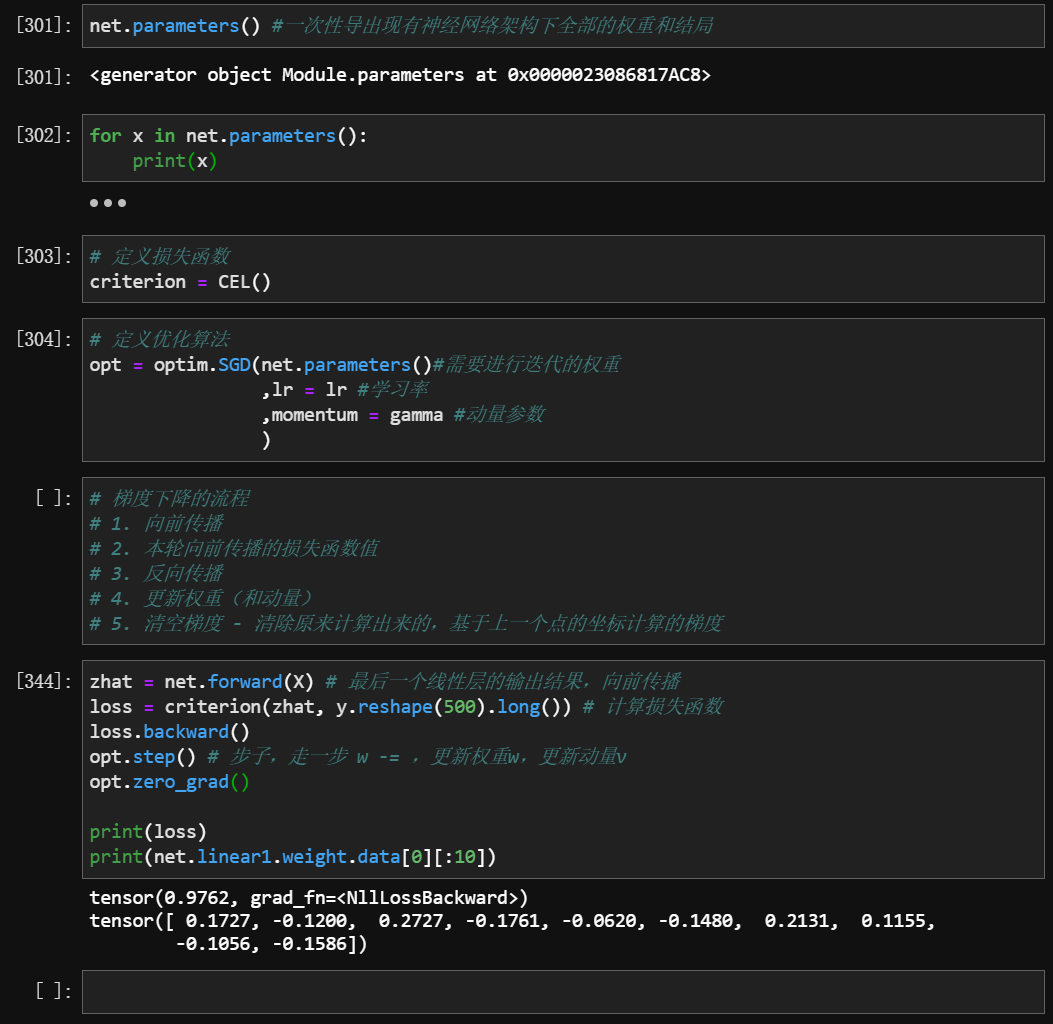
梯度下降的流程:
- 向前传播
- 本轮向前传播的损失函数值
- 反向传播
- 更新权重(和动量)
- 清空梯度 - 清除原来计算出来的,基于上一个点的坐标计算的梯度
三、开始迭代:batch_size与epoches
- 小批量梯度下降 (mini-batchSGD)
梯度下降法缺点:只能找到一个局部极小值,每次更新参数都需要使用所有的样本,如果对所有的样本均计算一次,当样本总数量特别大时,对算法的速度影响非常大。
因此便有了随机梯度下降 (SGD) ,它是对梯度下降算法的一种改进,且每次只随机取一部分样本进行优化,一般是2的整数次幂,范围是 32~256 ,以保证计算精度的同时提升计算速度,是优化深度学习网络中最常用的一类算法。
在深度学习中,SGD 通常指 小批量随机梯度下降 (mini-batchSGD)
- 为什么说 mini-batchSGD 更容易找到全局最优呢?
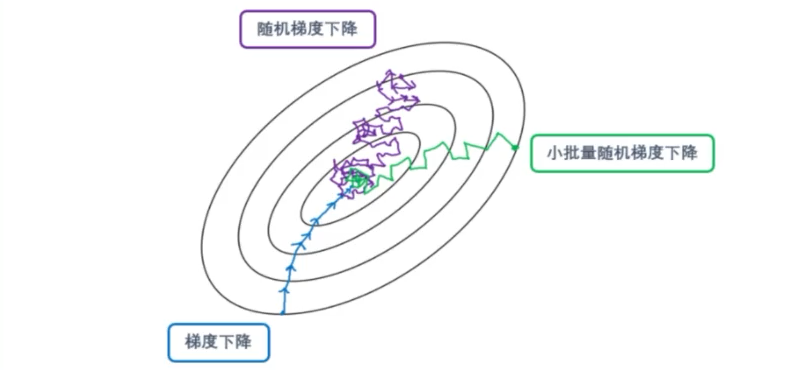
自问:为什么 SGD 可能会跳过局部最优,不会跳过全局最优吗?


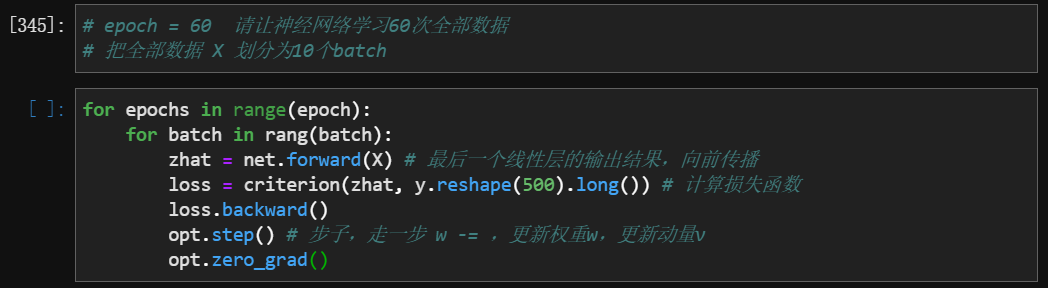
3.1 Tensordataset 与 DataLoader
Tensordataset
- 作用:数据打包
- 条件:被合并对象第一维度上的值相等
- 导包:
from torch.utils.data import TensorDataset- 用法:
TensorDataset(a,b,c)
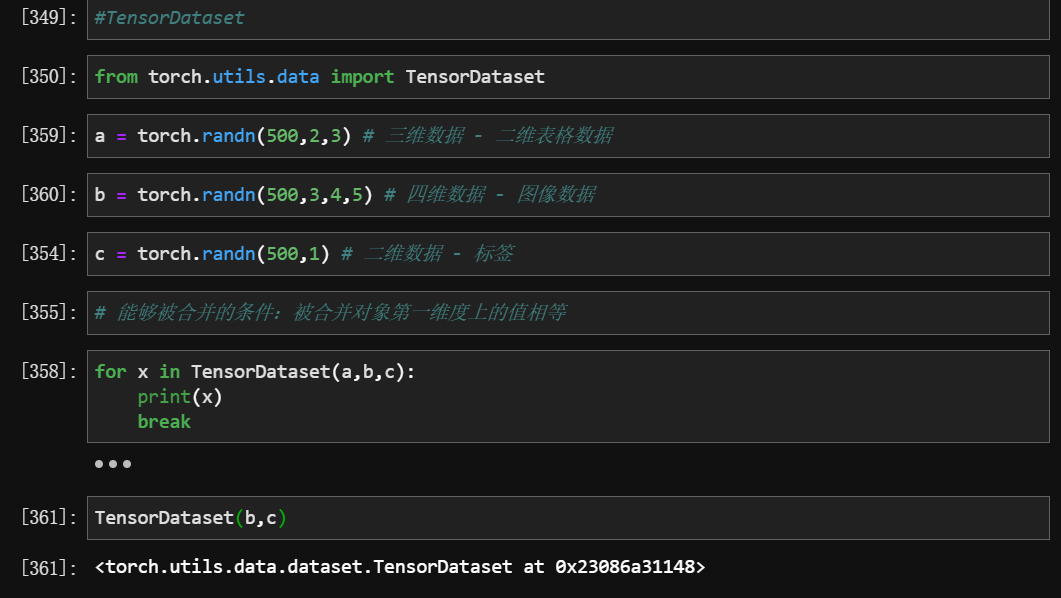
Dataloader
- 作用: 用来切割小批量的类
- 导包:
from torch.utils.data import DataLoader- 用法:
Dataloader(data)
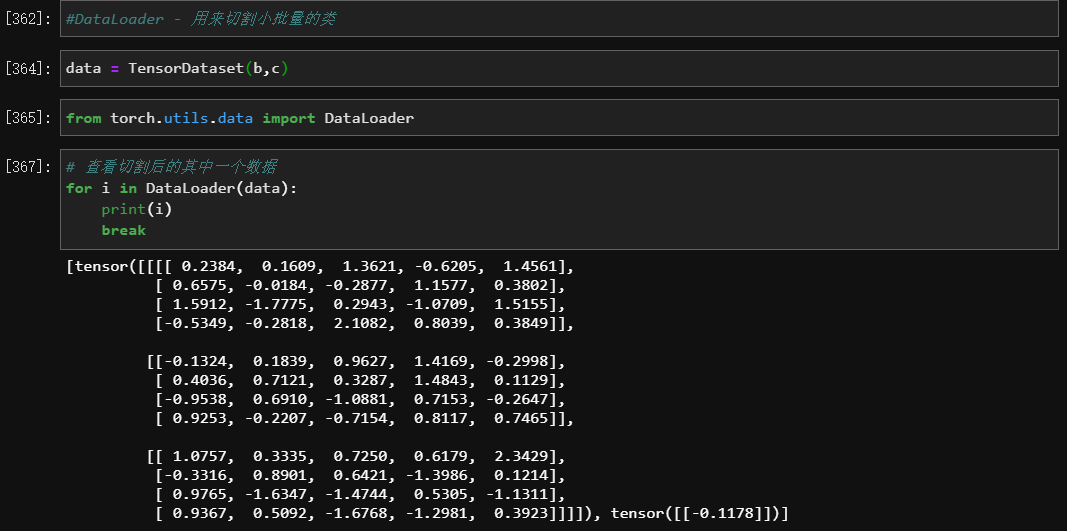
- 参数

- 处理后的结构
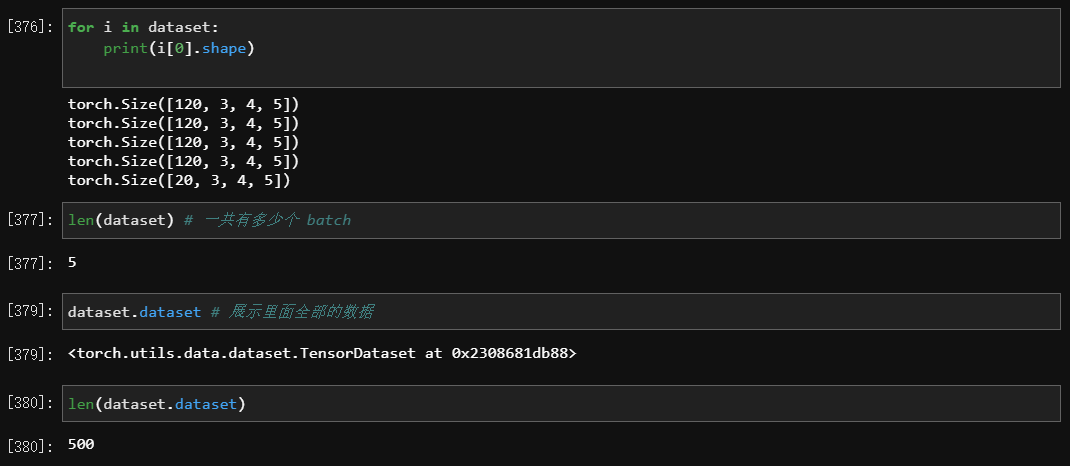
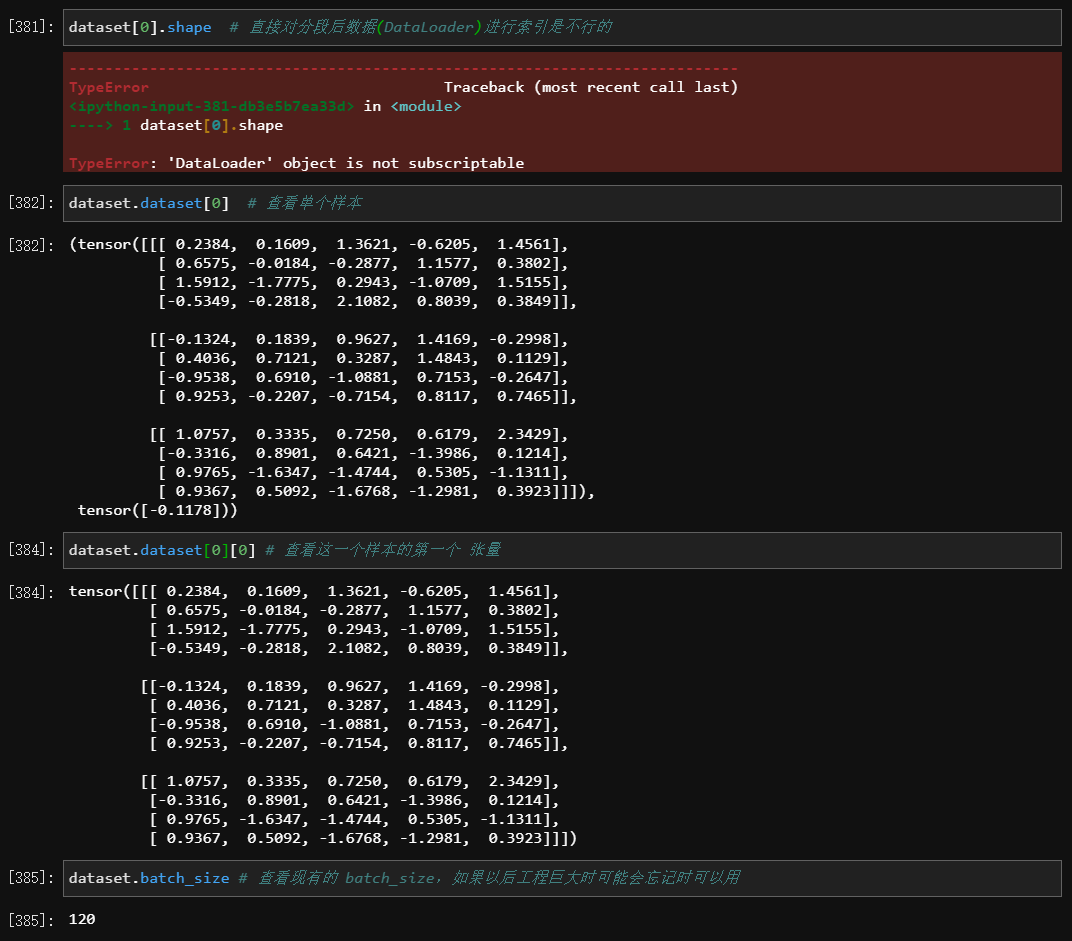
- 用 Sklearn 导入后怎么变成神经网络能够读取的小批量数据

- 用Pandas 导入后怎么变成神经网络能够读取的小批量数据
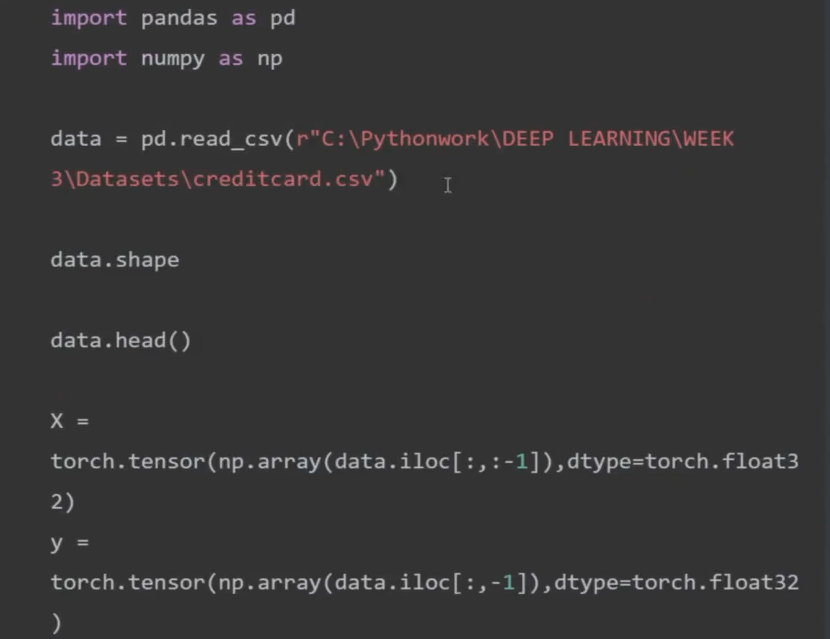
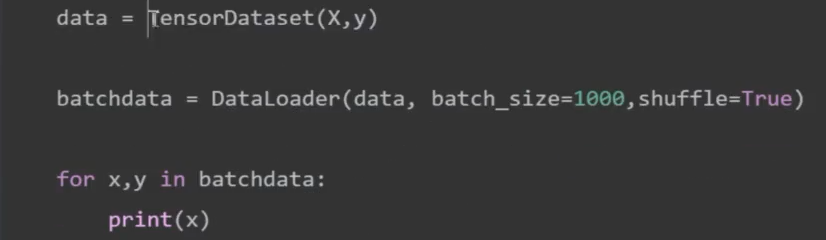
四、在MNIST-FASHION上实现神经网络的学习流程
4.1 流程
- 设置超参数:步长
lr、动量值gamma、迭代次数epochs、batch_size等信息,(如果需要)设置初始权重w0- 导入数据,将数据切分成 batches
- 定义神经网络架构
- 定义损失函数
L(w),如果需要的话,将损失函数调整成凸函数,以便求解最小值- 定义所使用的优化算法
- 开始在
epoches和batch上循环,执行优化算法:
- 调整数据结构,确定数据能够够在神经网络、损失函数和优化算法中顺利进行
- 完成向前传播,计算初始损失
- 利用反向传播,在损失函数
L(w)上对每一个w求偏导数- 迭代当前权重
- 清空本轮梯度
- 完成模型进度与效果监控 #
损失loss、准确率accuracy- 输出结果
1 | #实例化数据 |
4.2 代码
1 | import torch |
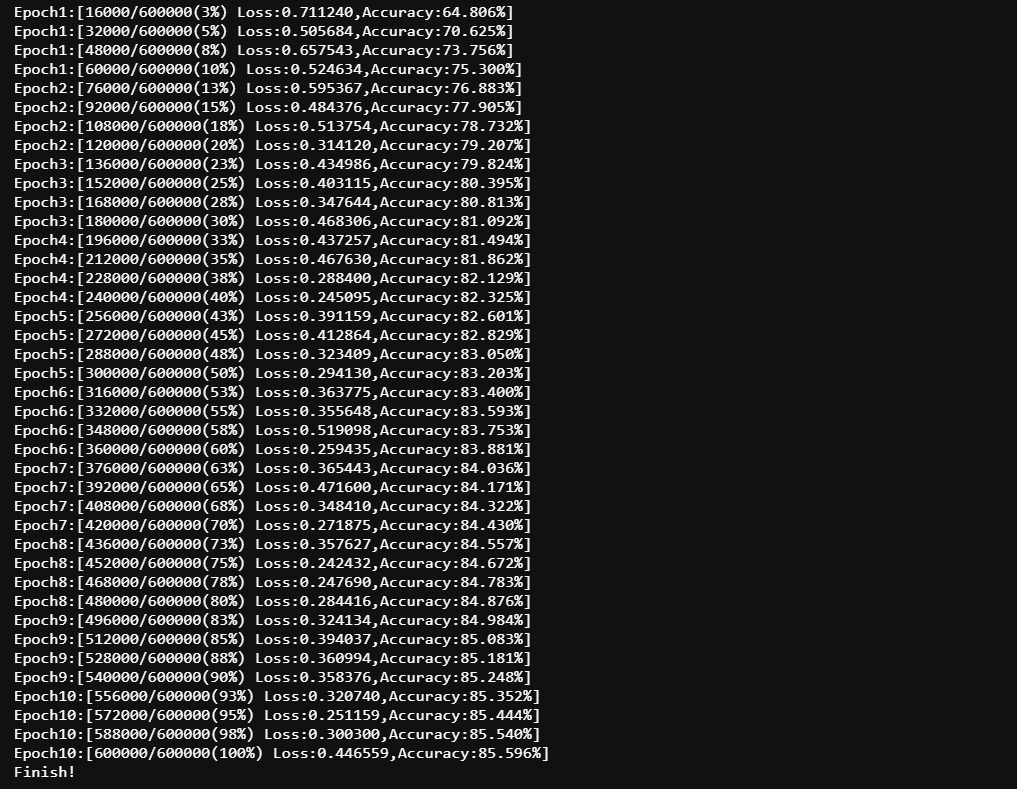
4.3 运行结果