一 、AutoGrad 的回溯机制与动态计算图
requires_grad属性:可微分性
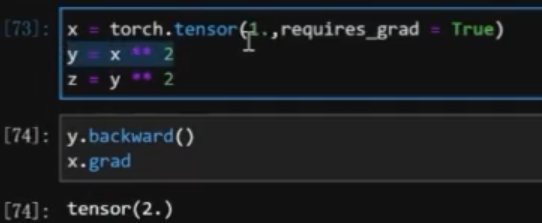
1 | x = torch.tensor(1., requires_grad = True) |
- y.n
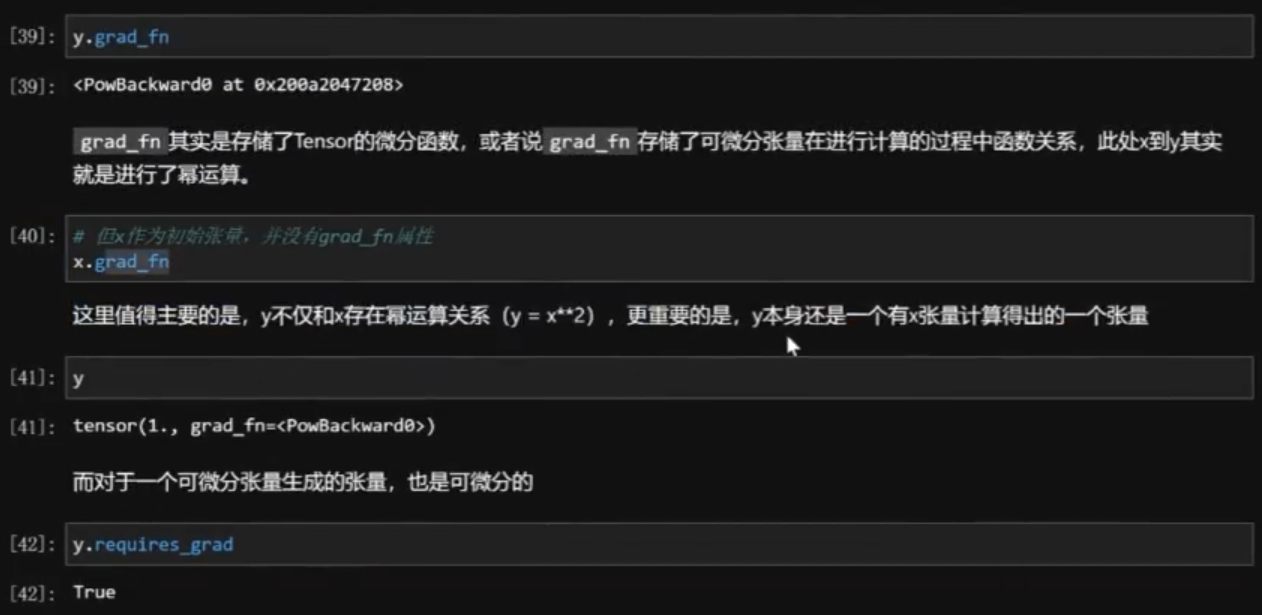
张量计算图
有向无环图
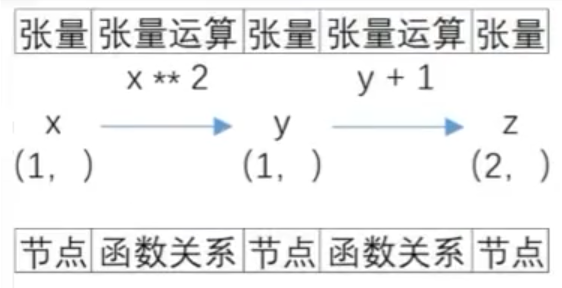
x:叶节点(与决策树不同):只有出边没后入边;
y:中间节点:既有入边,也有出边;
z:输出节点:只有入边,没有出边;
张量图的的动态性

二 、 反向传播与梯度计算
反向传播:函数关系的反向传播
- 在输出节点上进行反向传播,
z.backward()然后x.grad就可以查看 x = 1 的导数值- 只能
z.backward一次 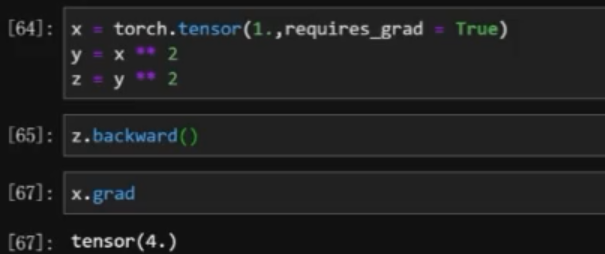
- 只能
- 也可以在中间节点上反向传播

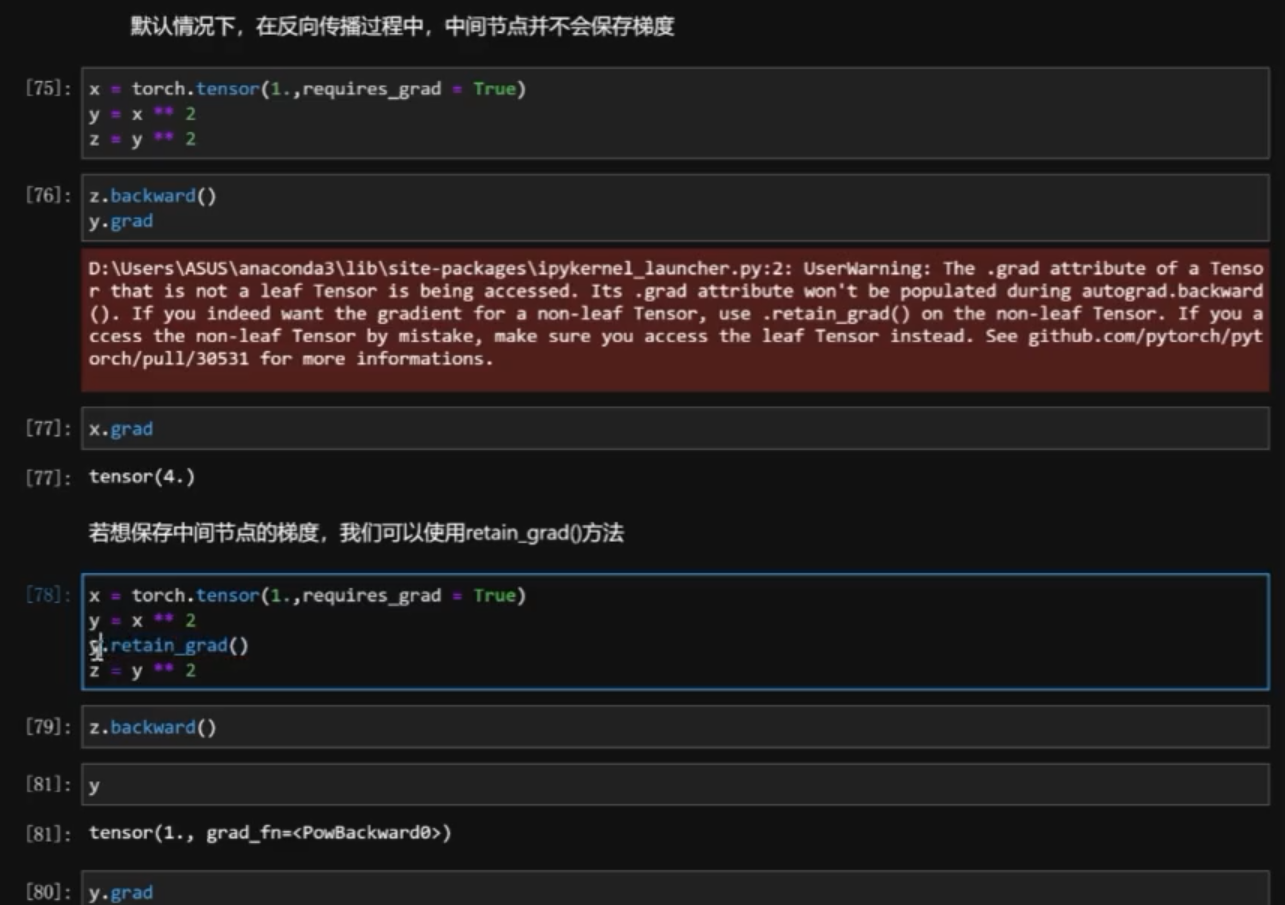
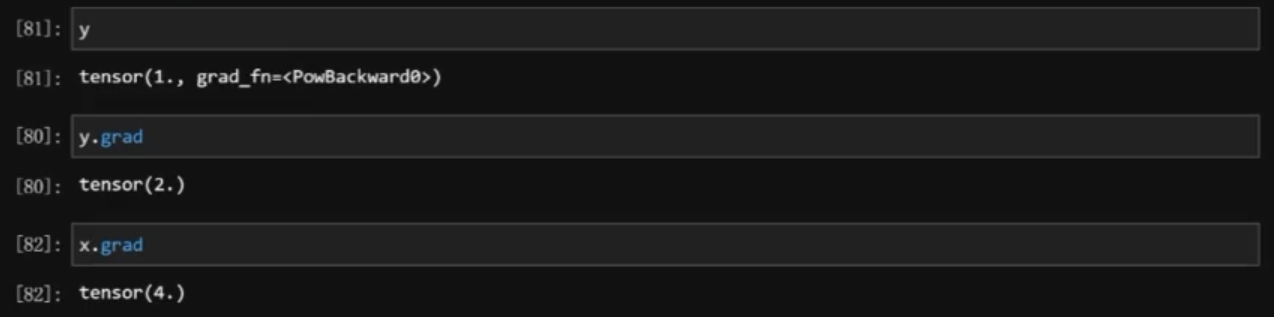
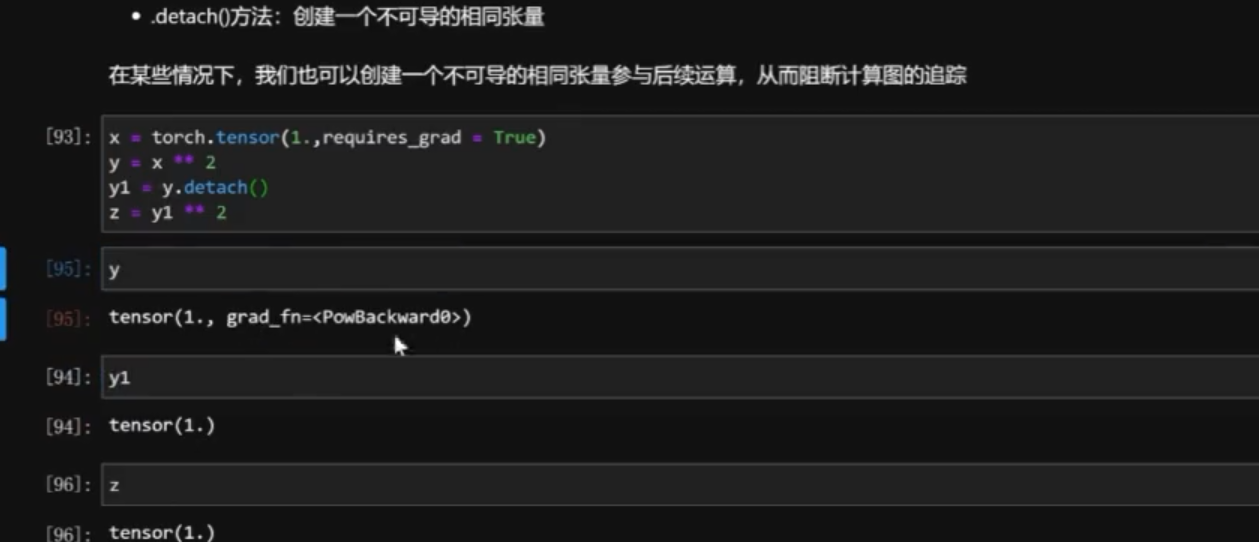
1 阻止计算图追踪
方法一:
with torch.no_grad()阻止计算图记录
从 z 开始不能微分了
方法二:
.detach()方法
2 识别叶节点
x.is_leaf查看- 存在问题:新创建的张量,还没有来记得加入到计算图中,查询结果都是
叶节点。
- 存在问题:新创建的张量,还没有来记得加入到计算图中,查询结果都是
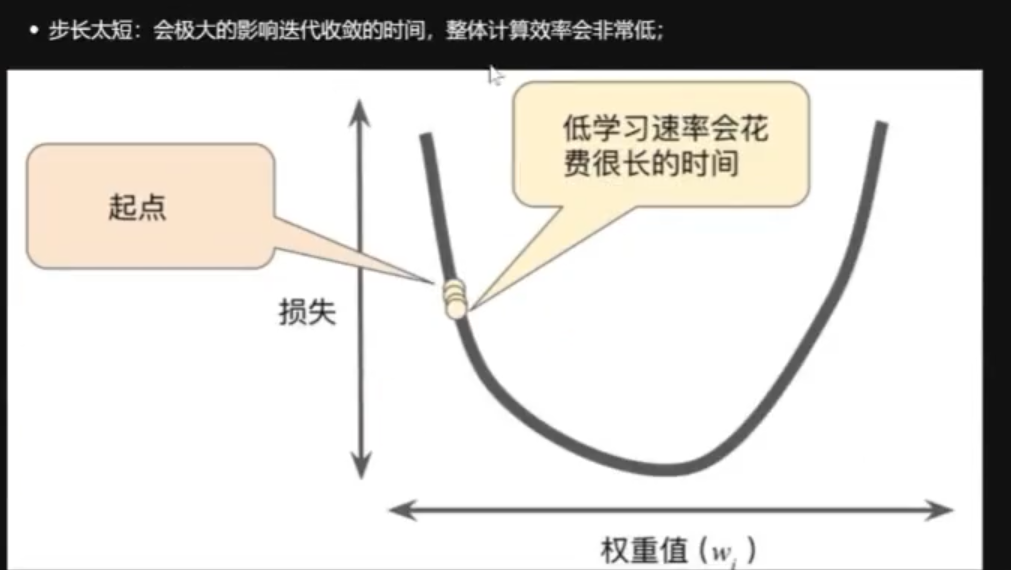
三、梯度下降的基本思想
1 最小二乘法的局限与优化
- 局限:
- 如果满足特定条件 ( X 满秩,不能共线 ),结果又快又好;
- 但条件苛刻,难以达到。
2 梯度下降的提心思想

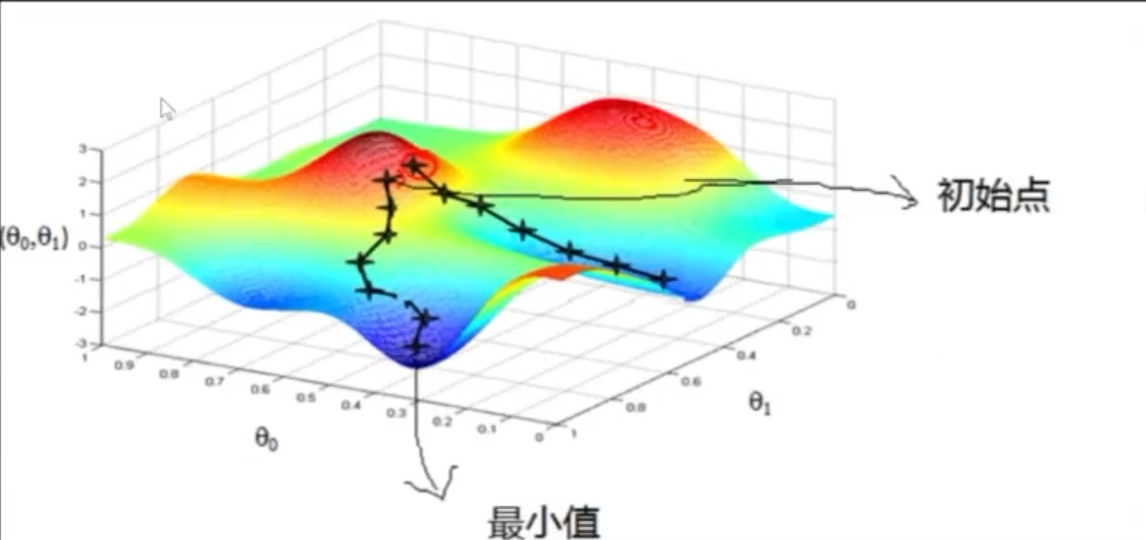
- 核心两个问题?
- 朝哪个方向移动?
- 梯度就是方向,梯度就向量,和高中物理向量无差别。
- 每一步移动多长?
- 步长 / 学习率:学习率 * 梯度 = 第一步步长
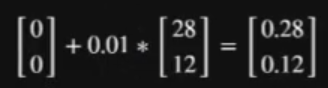

- 步长 / 学习率:学习率 * 梯度 = 第一步步长
- 朝哪个方向移动?
重新理解学习率: 初始点 0 ,终点 2,学习步长是 0.5 。
- 第一步:移动了(2 - 0)* 0.5 = 1,移动至:2 - 1 = 1 的位置;
- 第二步:移动了(2 - 1)* 0.5 = 0.5,移动至:1 - 0.5 = 0.5 的位置;
- 第三步:移动了(2 - 1.5)* 0.5 = 0.25,移动至:0.5 - 0.25 = 0.25 的位置;
- ……
理解步长 :